Что такое фактическое (эмпирическое) и теоретическое распределение? Давайте рассмотрим это на примере организации лотереи 1 из 6, т.е. будем бросать игральную кость — надо угадать один номер из 6. Если кто-то думает, что это совершенно не похоже на лотерею, то думаю я смогу вас переубедить и доказать, что аналогия совершенно полная. Любая числовая лотерея по сути та же игра в кости. Для получения статистики можем бросить 100 раз игральную кость или бросить сразу 100 игральных костей и подсчитать количество возможных вариантов, (а что если выпадет сразу 100 шестерок, и изменится ли что-то, если их сначала пронумеровать?). Ой, держите меня, меня куда-то не туда заносит, я не собираюсь здесь излагать всю теорию вероятностей.
Ну, как бы то ни было, пусть в результате розыгрыша 100 тиражей получили таблицу результатов:
Номер тиража Выпавшее число
100 3
99 4
98 6
……. ……
3 2
2 6
1 6
Упс… где-то что-то похожее мы уже видели.
Подсчитаем сколько раз выпадали номера 1 — 6 и запишем результаты в таблицу:
1 2 3 4 5 6 Всего:
21 19 14 17 14 15 100
Или в относительных частотах:
1 2 3 4 5 6 Всего:
0,21 0,19 0,14 0,17 0,14 0,15 1
Мы знаем, что теоретическая вероятность выпадения любого номера равна 1/6 или, что одно и тоже, таблица выпадения этих номеров например такая:
1 2 3 4 5 6 Всего:
10000 10000 10000 10000 10000 10000 60000
Или в относительных частотах:
1 2 3 4 5 6 Всего:
0,166667 0,166667 0,166667 0,166667 0,166667 0,166667 1
Теперь строим график:
График 1. Частота выпадения цифр 1-6.
На графике синие столбики – фактическое распределение, красная линия – теоретическое (все в относительных частотах).
Перейдем к лотереи Гослото 6 из 45 и подсчитаем сколько раз выпали номера 1– 45 (Excel нам в помощь. Аминь.) и получим первую глобальную таблицу:
Таблица 1. Количество выпадений номеров лотереи Гослото 6 из 45 после 1409 тиража.
Количество возможных комбинаций с одним номером равна:
(8145060 * 6) / 45 = 1086008
8145060 – количество возможных комбинаций лотереи Гослото 6 из 45,
(8145060*6) = 48870360 – общее количество номеров участвующих в создании 8145060 комбинаций,
В результате получаем таблицу:
Таблица 2. Общее количество выпадений номеров лотереи Гослото 6 из 45.
По этим таблицам строим график распределения:
График 2. Количество выпадений номеров лотереи Гослото 6 из 45 после 1409 тиража.
Прошу заметить, что все графики в моем анализе получаются именно по такой методике – по результатам проведенных тиражей создается таблица с фактическим распределением, далее создается эта же таблица с распределением в относительных частотах, далее создается таблица теоретического распределения и таблица теоретического распределения в относительных частотах. Таким образом, строятся 4 таблицы, на основании которых и получаем такие графики, а что делать без труда и пруда ухи не будет.
Теперь то же самое для лотереи Евромиллионы:
Таблица 3. Количество выпадения номеров лотереи Евромиллионы после 812 тиража.
Количество возможных комбинаций с одним номером равна:
(2118760 * 5) / 50 = 211876
2118760– количество возможных комбинаций лотереи Евромиллионы,
(2118760 *5) = 10593800 – общее количество номеров участвующих в создании 2118760 комбинаций,
В результате получаем таблицу:
Таблица 4. Общее количество выпадений номеров лотереи Евромиллионы.
По этим таблицам строим график распределения:
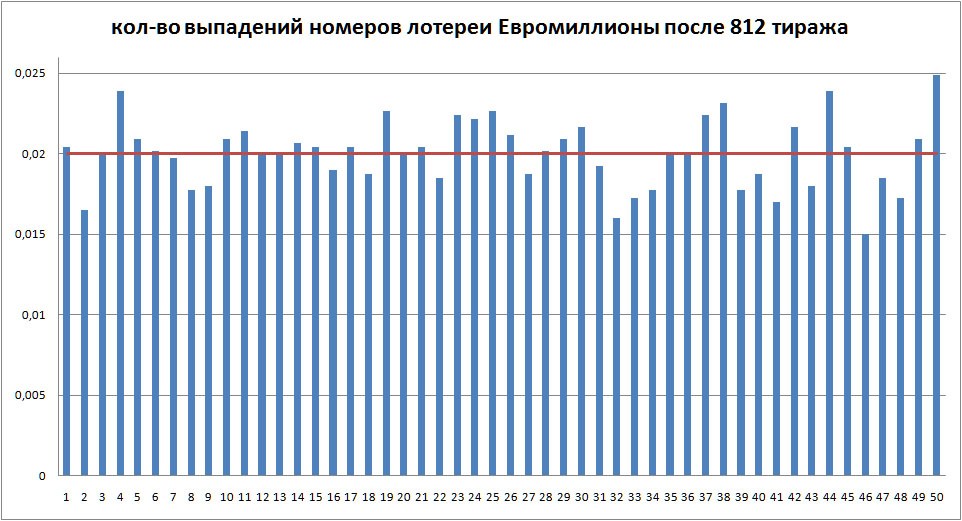
График 3. Количество выпадений номеров лотереи Евромиллионы после 812 тиража.
P.S. здесь не могу не привести цитату:
Задачи математической статистики
Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении методами теории вероятностей статистических данных — результатов наблюдений.
Первая задача математической статистики – указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов.
Вторая задача математической статистики – разработать методы анализа статистических данных в зависимости от целей исследования. Сюда относятся:
а) оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости случайной величины от одной или нескольких случайных величин и др.
б) проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен.
Итак, задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов (выделено мной).
Гмурман В.Е. Теория вероятностей и математическая статистика. глава 15. 9 издание 2003 г.
Источник: Исследование числовых лотерей методами математической статистики Ч.2