В предыдущей части исследования мы получили несколько очень веселых графиков (просто мечта статистика). Ну, а нам то, что с них? Отвечу – даже любой старшеклассник, с первого взгляда скажет, что все эти графики имеют вершины, а это значит, что их надо покорять. Ну что, кто со мной на Эверест…
Для того что бы было удобно объяснять, воспроизведу здесь несколько переделанную таблицу, которую я приводил в предыдущем посте «Количество выпадений номеров в каждой позиции лотереи Гослото 6 из 45 после 1409 тиража». Вся она тут не поместится, а надо ее внимательно изучить. Итак:

Таблица 1. Количество выпадений номеров в каждой позиции лотереи Гослото 6 из 45 после 1409 тиража (фрагмент).
Из приведенной таблицы следует, что в первой позиции количество выпавших номеров с 1 по 10 за 1409 тиражей составляет – 1118, а это почти 80% от всего количества. Теоретическое значение – 80,071847%. Т.е. другими словами на первые 10 номеров в первой позиции приходится 80% результатов всех тиражей, или, еще проще, примерно в каждых 8 тиражах из 10 в первой позиции выпадают номера с 1 по 10. Всего возможных номеров в этой позиции 40, поэтому номера 1- 10 составляют 25% от общего количества.
На графике, который я уже приводил в предыдущем посте, это соответствует закрашенной области:
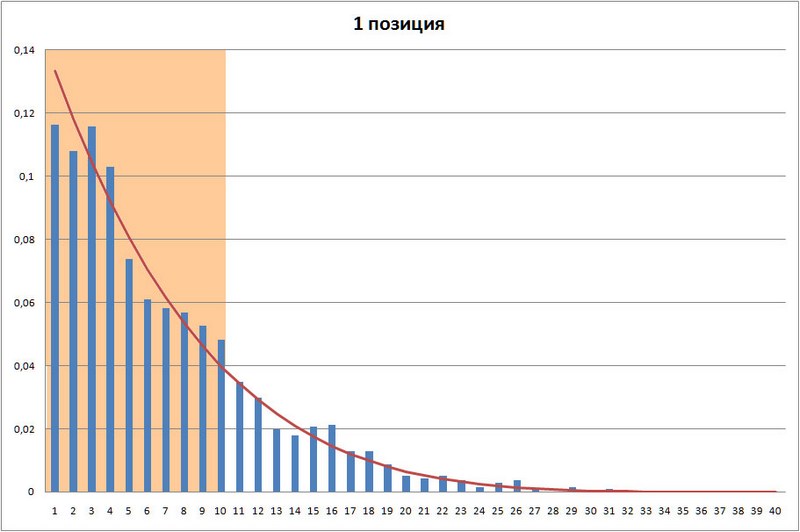
График 1. График распределения номеров в 1 позиции лотереи Гослото 6 из 45 после 1409 тиража.
Надеюсь, вы уже поняли, что этот же вывод следует сделать для номеров 36 – 45 в шестой позиции. Для этих номеров количество выпавших номеров за 1409 тиражей составляет 1139, что составляет 80,837473% от всего количества, и теоретическое значение так же, как вы уже наверно догадались равно – 80,071847%.
Во второй позиции (смотри таблицу 1) для номеров с 4 по 20 количество выпавших номеров за 1409 тиражей составляет 1170, что составляет 80,837473% от всего количества, сравните с теоретическим значением равным 80,516166%.
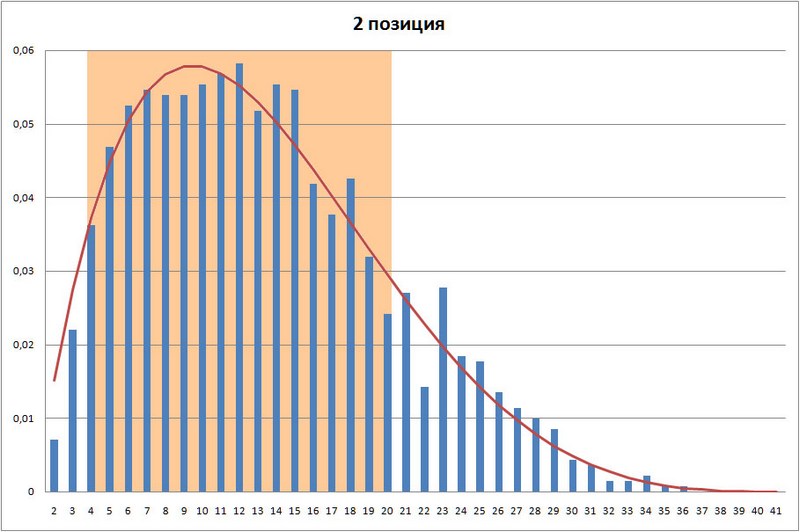
График 2. График распределения номеров в 2 позиции лотереи Гослото 6 из 45 после 1409 тиража.
Для 5 позиции номера с 26 по 42 количество выпавших номеров за 1409 тиражей составляет 1123, что составляет 79,701916% от всего количества (теоретическое значение 80,516166%).
Для третьей позиции номера с 10 по 28 количество выпавших номеров за 1409 тиражей составляет 1092, что составляет 77,501774% от всего количества. Теоретическое значение, поверьте мне на слово, – 78,280823%. Для 4 позиции номера с 18 по 36 — количество выпавших номеров – 1098, что составляет 77,927608% от всего количества.
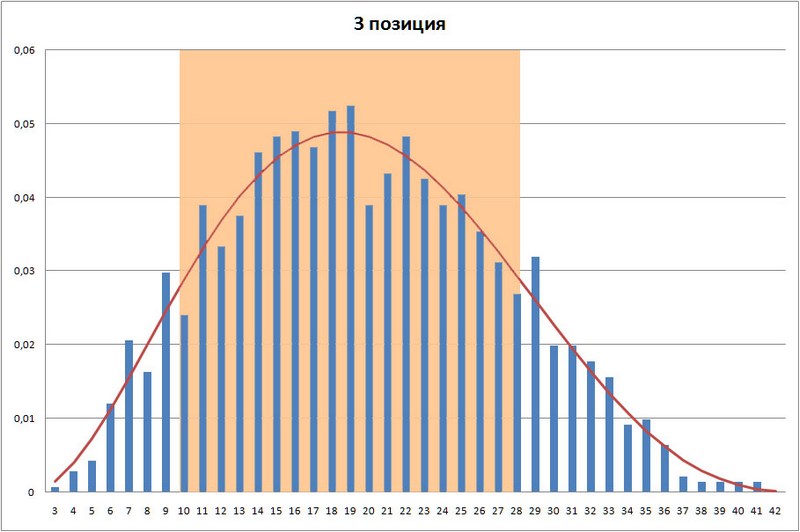
График 3. График распределения номеров в 3 позиции лотереи Гослото 6 из 45 после 1409 тиража.
На этом пока все с этими графиками.
А теперь прошу заметить, что наша таблица поможет нам подсчитать количество четных и нечетных номеров для каждой позиции.
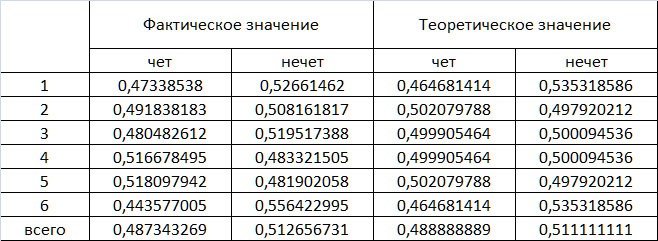
Таблица 2. Количество выпадения четных и нечетных номеров для каждой позиции лотереи Гослото 6 из 45 после 1409 тиража в относительных единицах.
Надеюсь вы поняли на что я намекаю. Правильно в каждом тираже на каждой позиции может быть только Чет или Нечет, а вам даже самый ненормальный игрок казино не посоветует ставить сразу на обе.
Очень кратко, те же графики для лотереи Евромиллионы (таблица и графики в предыдущем посте):
1 позиция. Номера с 1 по 13 фактическое количество выпавших номеров за 812 тиражей – 651, что составляет 80,1724% от общего количества, теоретическое значение – 79,4268%.
5 позиция. Номера с 38 по 50 фактическое количество выпавших номеров за 812 тиражей – 650, что составляет 80,0493% от общего количества, теоретическое значение – 79,4268%.
2 позиция. Номера с 2 по 24 фактическое количество выпавших номеров за 812 тиражей – 648, что составляет 79,803% от общего количества, теоретическое значение – 79,9609%.
4 позиция. Номера с 27 по 49 фактическое количество выпавших номеров за 812 тиражей – 640, что составляет 0,788177% от общего количества, теоретическое значение – 79,9609%.
3 позиция. Номера с 14 по 37 фактическое количество выпавших номеров за 812 тиражей – 668, что составляет 82,266% от общего количества, теоретическое значение – 79,4013%.
Между нами, — лотерея Евромиллионы просто обожает этот диапазон, и как видно из графика явно за счет правого диапазона.
Здесь просто не могу еще раз не полюбоваться на этот график:
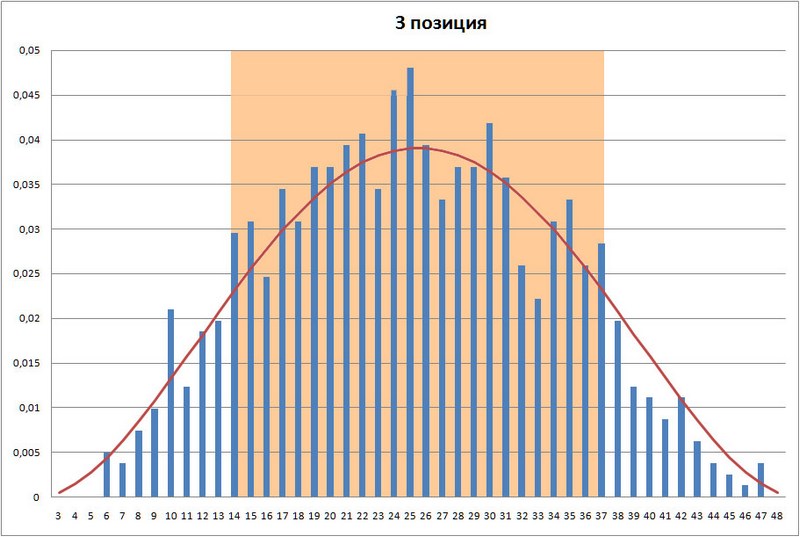
График 4. График распределения номеров в 3 позиции лотереи Евромиллионы после 812 тиража.
Количество четных и нечетных номеров для каждой позиции лотереи Евромиллионы.

Таблица 3. Количество выпадения четных и нечетных номеров для каждой позиции лотереи Евромиллионы после 812 тиража в относительных единицах.
А вот из этой таблицы видно относительное предпочтение лотереи Евромиллионы нечетных номеров во второй позиции и четных номеров в пятой.
Теперь только для экстремалов любителей Excel.
Давайте попробуем определить, как располагаются четные и нечетные номера в каждом тираже, а также определить их распределение, причем сделать это не прибегая к программированию. Для этого сначала составим таблицу четных и нечетных номеров:
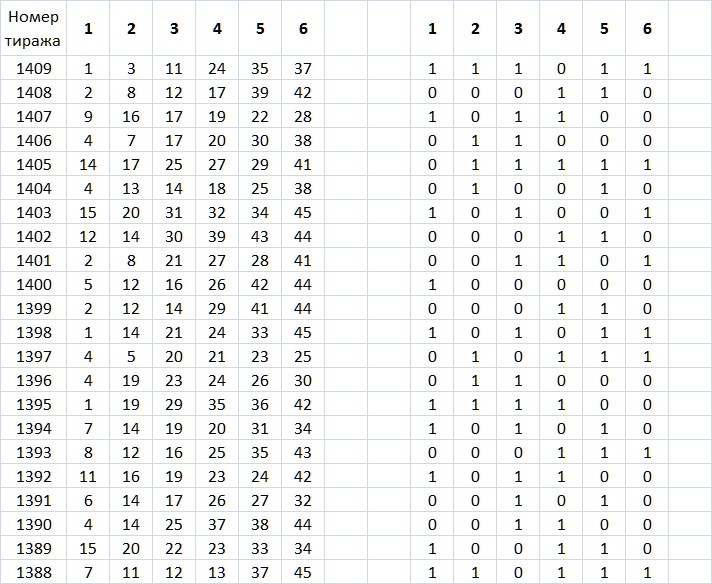
Таблица 4. Определяем четные и нечетные номера лотереи Гослото 6 из 45.
Если кто, забыл, напомню формулу для ячейки =ЕСЛИ(ЕНЕЧЁТ(B2)=ИСТИНА;1;0).
Так, так, так…, что-то знакомое, матрица прям какая-то. Прям код да Винчи какой-то, но с кодами мы работать умеем. Идем дальше, эту матрицу преобразуем в следующую таблицу:

Таблица 5. Преобразование кода выпадения четных и нечетных номеров лотереи Гослото 6 из 45.
Надеюсь, вы догадались, что используется формула — =ЕСЛИ(J2=1;32;0),
J2 – номер соответствующего столбца в Excel.
Ну, а дальше дело техники, необходимо всего лишь подсчитать сколько раз выпадал тот или иной код, делать это можно разными способами (на любителя), я чтоб было понятнее, сделал это так:
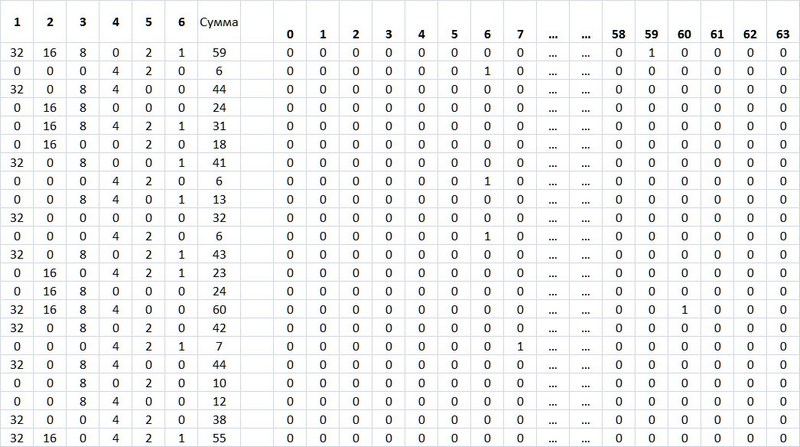
Таблица 6. Подсчитываем сколько раз, выпадали коды распределения четных и нечетных номеров лотереи Гослото 6 из 45.
Используем формулу Excel =ЕСЛИ(W2=0;1;0) для 0 столбца.
W2 — номер столбца «Сумма» (для ячейки второго ряда с номером столбца 59 формула будет -=ЕСЛИ(W2=59;1;0)).
Далее суммируем количество единиц по каждому столбцу и voilà:

Таблица 7. Количество выпадений кодов распределения четных и нечетных номеров лотереи Гослото 6 из 45 после проведения 1409 тиража.
Ну, а теперь долгожданная гистограмма:
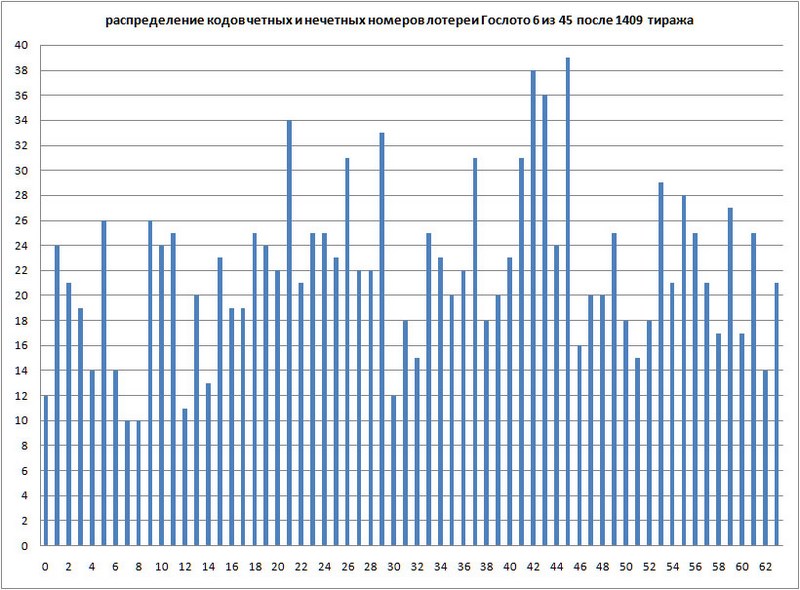
График 5. Распределение кодов четных и нечетных номеров лотереи Гослото 6 из 45 после 1409 тиража.
Это распределение просто требует статистического анализа (для начала, определить какое это распределение, и параметры этого распределения), но для меня этот график сейчас не главное (может, когда-нибудь вернусь к нему).
То же самое для лотереи Евромиллионы:
Таблица 8. Количество выпадений кодов распределения четных и нечетных номеров лотереи Еромиллионы после 812 тиража.

График 6. Распределение кодов четных и нечетных номеров лотереи Евромиллионы после 812 тиража.
Сюда же до кучи еще несколько графиков:
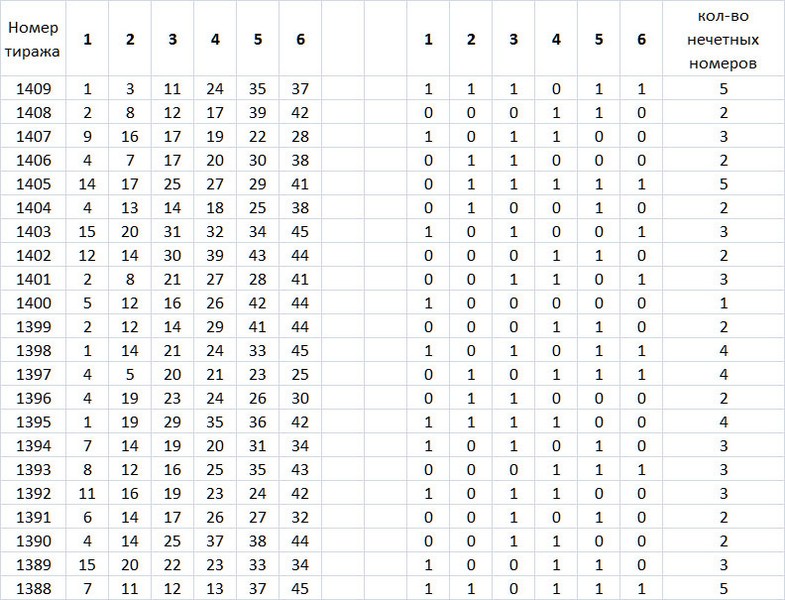
Таблица 9. Количество нечетных номеров лотереи Гослото 6 из 45.
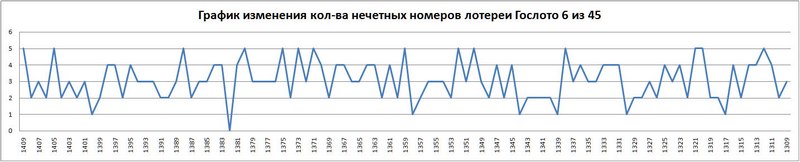
График 7. График изменения количества нечетных номеров лотереи Гослото 6 из 45.
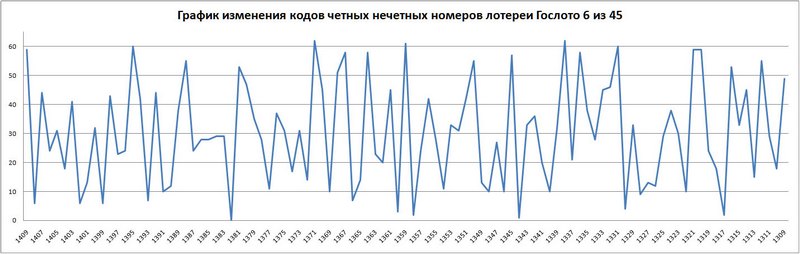
График 8. График изменения кодов четных и нечетных номеров лотереи Гослото 6 из 45.

График 9. График изменения количества нечетных номеров лотереи Евромиллионы.
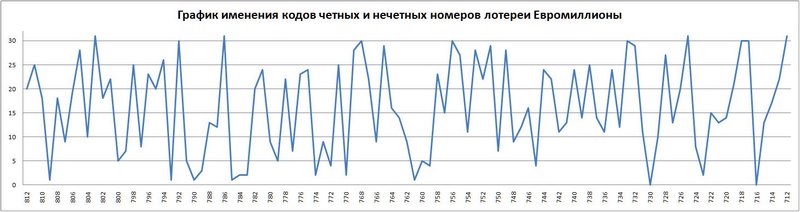
График 10. График изменения кодов четных и нечетных номеров лотереи Евромиллионы.
Из графика изменения кодов четных и нечетных номеров лотереи Гослото 6 из 45 видно, что код на протяжении 100 тиражей повторился 3 раза, а в лотереи Евромиллионы, при вдвое меньшем размахе только один раз.
Источник: Исследование числовых лотерей методами математической статистики Ч.4